Introdução
A primeira pergunta que fazemos quando abordarmos o conceito de fração é:
– O que é fração?
Fração é uma forma de dividir um inteiro em partes iguais. Podemos exprimi-la através de representação figural ou por meio de representação fracionária.
A Base Nacional Comum Curricular (BNCC) recomenda que esse assunto seja abordado no ensino básico e destaca um dos objetivos os quais o processo de ensino e de aprendizagem da matemática deve alcançar:
(EF06MA09) Resolver e elaborar problemas que envolvam o cálculo da fração de uma quantidade e cujo resultado seja um número natural, com e sem uso de calculadora.
Para alcançar esse objetivo faz-se necessário que o(a) aluno(a) conheça e compreenda o conceito de fração e como representá-lo. Desejamos contribuir para que esse objetivo seja alcançado, para isso, apresentamos e discutimos sobre o conceito de Fração e suas representações.
Destacamos, também, os cuidados que o(a) aluno(a) deve ter ao transformar a representação figural para fracionária.
Representação fracionária
A representação fracionária é expressa por um número sobre o outro separados por um traço. Intitulamos o número de cima de numerador e o de baixo de denominador. O numerador equivale a quantidade de partes a qual estamos considerando e o denominador refere-se ao total de partes iguais que o inteiro foi dividido. O traço é a linha da divisão da representação fracionária, em alguns casos, é utilizado o sinal / para representá-lo.
Veja o exemplo (figura 1) em que dividimos um inteiro em três partes iguais e consideramos duas partes. Essa fração é intitulada de dois terços.

Representação figural dividida em partes iguais
A representação figural é expressa por uma figura dividida em partes iguais. Algumas dessas partes são pintadas ou hachuradas para destacar o numerador. O total de partes em que a figura foi dividida representa o denominador.
Veja o exemplo (figura 2) da representação figural da fração dois terços. Dividimos o círculo em três partes iguais, representando o denominador, e pintamos duas partes, referindo-se ao denominador.
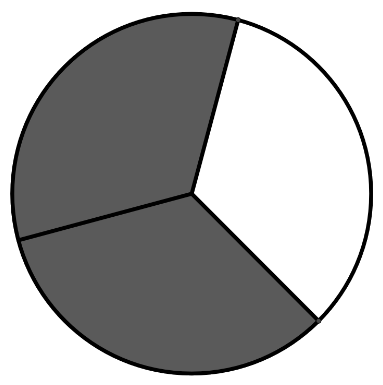
Representação figural dividida em partes não iguais
Vale ressaltar que em algumas atividades matemáticas a figura não está dividida em partes iguais. Neste caso, devemos efetuar outras divisões para que todas as partes representem a mesma área.
Veja o exemplo do retângulo abaixo (figura 3). A figura foi dividida em quatro partes e pintada uma. Porém, não podemos dizer que ela representa a fração \frac{1}{4} (um quarto) porque suas partes não possuem a mesma área.

O que devemos fazer? Devemos dividir a figura de modo a obtermos partes que tenham a mesma área.
A primeira divisão que efetuamos foi traçar um segmento de reta paralela em relação aos lados menores do retângulo, iniciando e terminando no ponto médio dos lados maiores (figura 4). Dessa maneira, obtemos quatro retângulos menores de mesmo tamanho.

Observando com mais cuidado a figura 4, podemos perceber que dois dos quatro retângulos menores estão divididos por um segmento de reta denominado diagonal. A diagonal divide o retângulo em dois triângulos retângulos de mesma área.
Efetuamos essa mesma divisão nos outros dois retângulos menores. Veja a figura 5 como ficou o retângulo maior com essas divisões.

Observando a figura 5, podemos notar que o retângulo foi dividido em oito triângulos retângulos cujas áreas possuem as mesmas medidas. Dessa maneira, pode-se afirmar que a figura 5, consequentemente a figura 3, representam a fração \frac{1}{8} .
Frações equivalentes
Outro ponto que merece destaque são as frações equivalentes. Afinal, o que são frações equivalentes?
Frações equivalentes são frações que representam um mesmo valor numérico. Por exemplo, as frações \frac{1}{4} (um quarto) e \frac{2}{8} (dois oitavos) são equivalentes.
Ao efetuarmos a operação 1 ÷ 4 obtemos 0,25. Assim a fração \frac{1}{4} representa o valor numérico 0,25.
O resultado da operação 2 ÷ 8 é 0,25. Dessa maneira a fração \frac{2}{8} representa o valor numérico 0,25.
Resumindo, pode-se afirmar que \frac{1}{4} e \frac{2}{8} são frações equivalentes pois representam um mesmo valor numérico: 0,25.
Por que tocamos nesse assunto?
Responderemos a esse questionamento fazendo uma outra pergunta. Podemos afirmar que a figura 6 representa a fração \frac{1}{4} ?

Observando com mais cuidado a figura 6, nota-se que o retângulo foi dividido em oito partes iguais e estamos considerando duas. Assim, pode-se afirmar que tal figura representa a fração \frac{2}{8} .
Acrescenta-se a esse contexto a afirmação de que as frações \frac{2}{8} e \frac{1}{4} são equivalentes. Assim, podemos dizer que a figura em questão também representa a fração \frac{1}{4} .
Considerações finais
Finalizamos esse texto destacando a importância de analisarmos com cuidado a representação figural de uma fração. Antes de afirmar que uma determinada figura representa tal fração, faz-se necessário verificar se as partes em que a figura foi dividida têm a mesma área. Além disso, em algumas situações, devemos lançar mão dos conceitos de frações equivalentes.
Aprecie nossos poemas
Formulário de comentários
Informamos que ao deixar o seu comentário você está ciente de que as informações preenchidas no formulário, o endereço de IP e os dados do navegador serão encaminhados ao responsável do website.
Após a aprovação, as informações preenchidas nos campos “NOME” e “COMENTÁRIOS” estarão visíveis ao público.
Você pode solicitar a remoção de tais informações a qualquer tempo através do formulário de contato do website ou através do e-mail <wilsonmonteiro@outlook.com>.
Para maiores informações acesse nossa Política de Cookies e de Privacidade.
